从物理模型上来讲，我们可以很简单地就设想出一个单自由度的振动模型，比如弹簧振子。
当我们给弹簧一个初速度，弹簧就会周期性的摆动，拥有往复的位移。
而波动，是在连续介质中不同位置处振动形式的传播。
甩鞭
设想我们在鞭子的首端施加一个向下的力，显然，力作用的质点会向下运动，由于鞭子是一个整体，其上各质点间的相互作用会带动相邻的质点一个接一个地向下运动，直至传至鞭子末端。
在鞭子中振动的传播，就形成了波。
应力波也是一种波动形式，就是说应力、应变状态的变化以波的方式传播。
也就是说，应力和应变也是在质点中依次传播的。
同样以鞭子类似，开始的质点拥有一个应力应变状态，各质点间的相互作用带动相邻的质点一个接一个地获得这种应力应变状态，直到传至鞭子末端。这时，质点的应力应变状态可以通过甩鞭时我们能看见的位移想象，总之是进行了一个物理量的传递。就是说，整个物体的应力应变状态变化是需要时间的，这就是惯性效应。
传播的速度就是波速，和波动一样。
可以想象，如果施加力的源头自身也有速度，并且越来越快超过音速，比如爆炸，后产生的波追上前面的波，就会在传播过程中的某个位置追上形成叠加，这个位置就会发生剧烈的振动，具有巨大的能量，这种波就成为了冲击波。
考虑压缩波的传播。
如图所示的细长杆，在左端突然作用一个均匀分布的压力F。
撞击的瞬间，杆端的薄层将产生一个均匀压缩，薄层获得向右的速度，这个压缩一层接一层地传递，直到杆的末端。
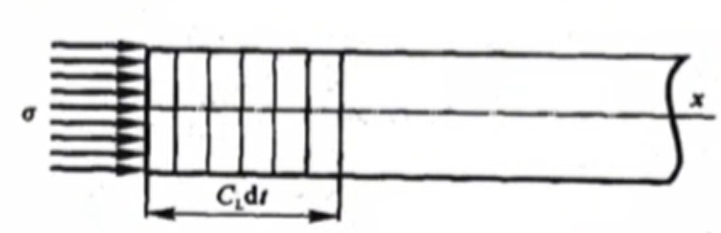
圆柱杆的冲击压缩
压缩波开始以某个速度 CL 沿杆向x 向移动，即经过时间dt后，杆端的长度为dl=CLdt的部分将受到压缩，而其余部分还未压缩，保持静止的初始状态。
根据冲量定理，以这一段杆为研究对象
F dt=ρA dl v
即 σ=ρCL v，其中ρCL称为波阻抗。
要注意区分CL 和 v，对于同一种介质，CL是在此介质中应力波传播的波速，值是恒定的；而 v是物质点的速度，大小和方向与应力的大小和方向有关。
实际上这个设想的模型是经过简化的，关于应力波方程的解法其实是通过解二阶偏微分方程得到的。
如何区分一维纵波中的压缩波和拉伸波呢？
1）从应力的角度，压缩波产生负的应力，而拉伸波产生正的应力。
2）从物质点运动速度和波传播方向来看，压缩波中物质点速度方向和波传播的方向一致，而拉伸波两者方向相反。
假设一根均匀等截面的细长弹性杆，遵循一维假定和应变率无关假定。
一维假定保证杆在变形中横截面保持不变，沿截面只有均匀分布的轴向应力，即各物理量只是X和t的函数，问题转化为一维问题。
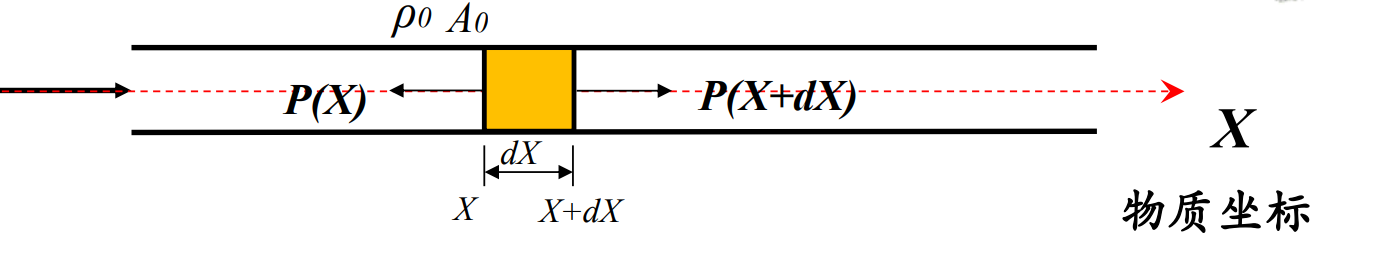
应变率无关假定保证材料的应力和应变唯一对应，在冲击载荷的某一应变率范围内具有平均意义上的唯一的动态应力应变关系。
求解这个问题，即求解X+dX截面上的状态，可以利用三个控制方程：
运动学条件：连续方程/质量守恒方程
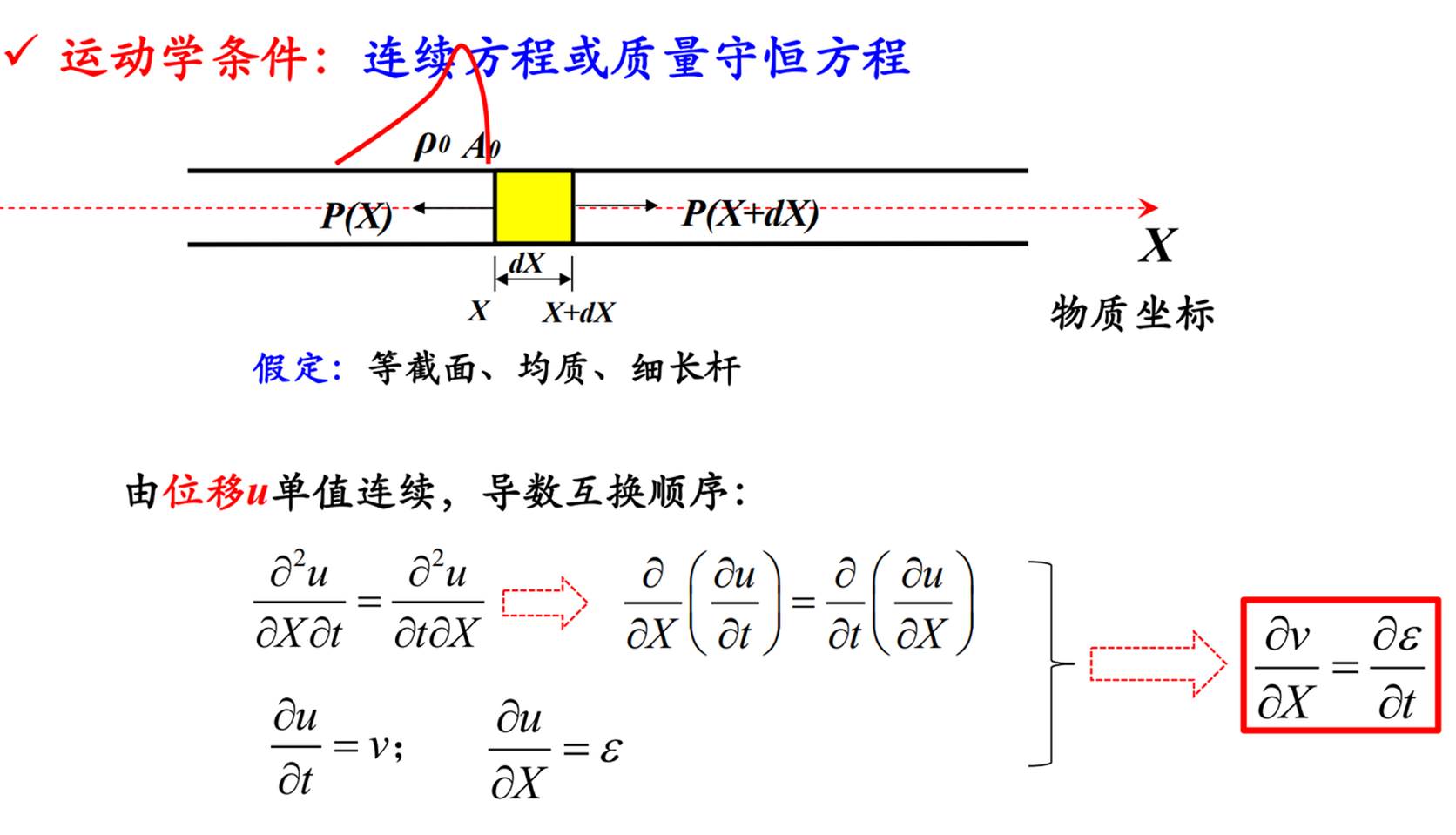
动力学条件：运动方程/动量收获方程
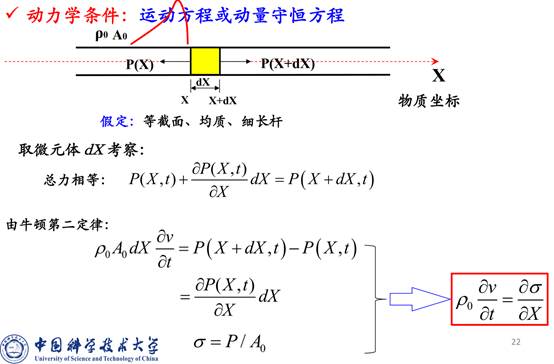
本构关系：本构方程/物性方程
从而可以推导出二阶偏微分的波动方程。
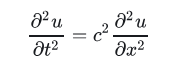
其通解形式如下
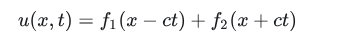
其中，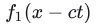
表示波沿着 + X方向传播，即右行波；
则表示左行波。
对上式求偏导数，也可以得到应力波的传播公式：
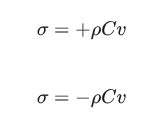
分别用于右行波和左行波。
以上方程是建立在物质坐标的，也可以转化为空间坐标，可以直接通过空间微商和物质微商进行转化，也可以通过在空间坐标中以控制体积dx作为研究对象，通过流量的方式重新建立以上三个控制方程。
如果波一直沿着同一种杆传播，那么它会一直进行下去。
如果传播过程中，介质发生改变，传递过来的入射波就会在介质截面的交界处发生透反射。
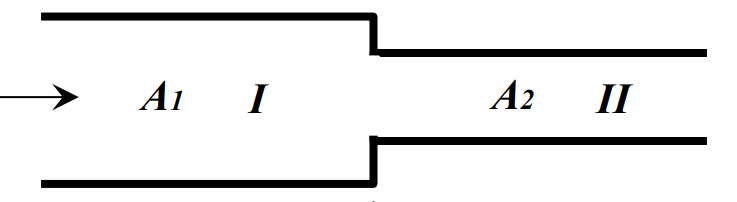
已知变截面杆为一个整体，截面两侧总的作用力和速度应该相等。
反射波和入射波传播方向相反。
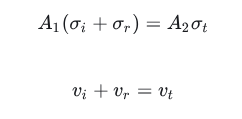
利用纵波的传播公式：
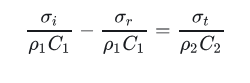
联立方程求解，可以得到
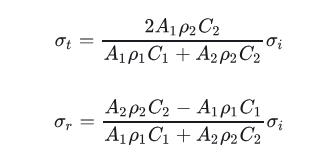
当两杆波阻抗相同，三波的关系如下：
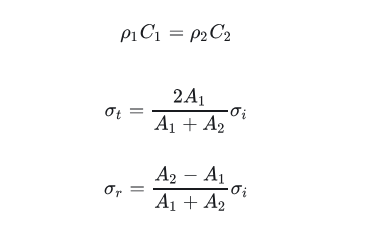
类似的，当两杆面积相同，三波关系也可简化。
值得一提的是，反射波的传播方向是不会变化的，始终是入射波的反方向，此处表现为左行波，应力与速度始终满足左行波的传播公式。
反射波的应力和速度的正负值，则代表拉/压应力和对应应力下物质点的运动方向。
假设入射波是压缩波，反射波和入射波同号，则同为压缩波，起到应力加载的作用；反射波和入射波异号，则成为拉伸波，起到应力卸载的作用。
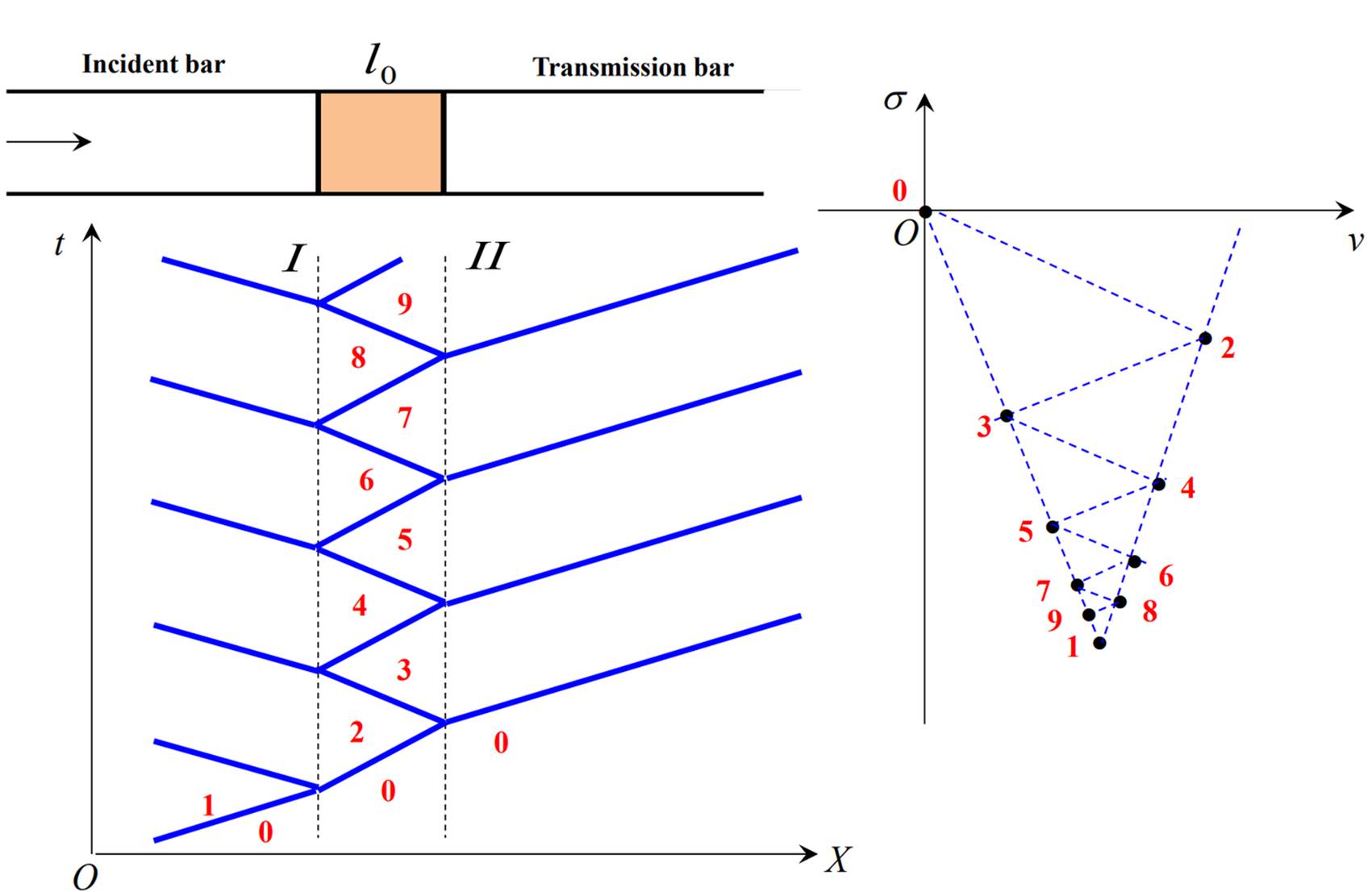
入射杆传入的脉冲压缩波，在入射杆、试样和透射杆中来回透反射。
对于试样来说，在很短的时间内，经过多次透反射，应力和应变状态就能趋于稳定。
各杆的弹性模量已知，且屈服应力应该足够高，使得撞击只在杆中产生弹性波，幅值可用应变片测定，且可重复使用。但当弹性压缩波穿过入射杆进入试件中，该脉冲的应力幅值应足以使试件发生塑性变形。一部分脉冲穿过试件进入透射杆，一部分脉冲反射回反射杆，在两杆适当位置上粘贴应变片，可以测得入射应力和透射应力随时间的变化曲线。这样可以直接测定入射脉冲 、透射脉冲 和反射脉冲 ，从这些数据得到试件中应力、应变和应变率的关系。
分离式Hopkinson压杆实验结果分析
一维弹性波假设：假设应力脉冲在压杆中为无畸变的以为弹性波。
忽略压杆材料的应变率效应，利用简单的一维弹性波理论直接得到试样的应力和应变。
一维应力状态下，压杆表面应变计测量的轴向应变才可以代表整个截面 个各点的轴向应变，才可以认为杆中应变计位置测量受力状态、应变与试样端面完全一样。
试样的应力/应变均匀性假设：由于试样很短，假设在很短的时间内试样长度方向的应力/应变均匀化。
在均匀性假设下，可以忽略试样的应力波效应，认为试样在均匀应力作用下变形。
试样的平均应力和压杆端面变形得到的试样平均应变才可以反映材料的真实力学性能。
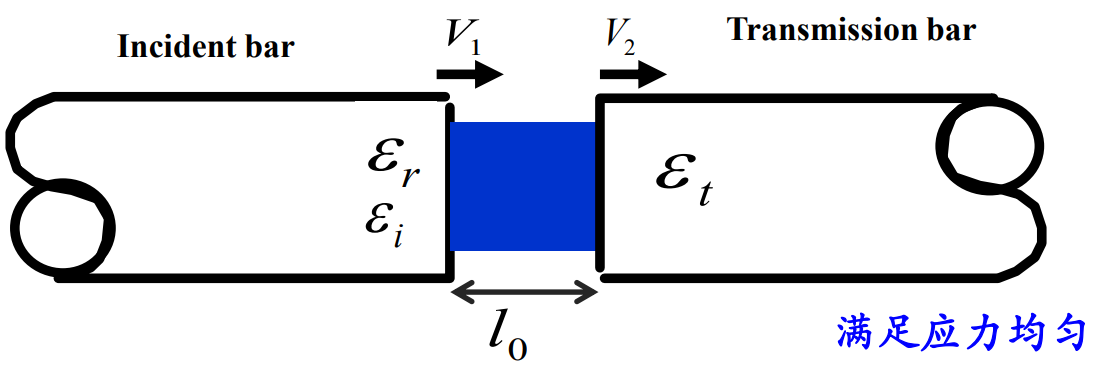
由试样两端应力和速度场，可以得到试样中的应力-应变曲线。
先由试样两端的速度差计算试样的压缩应变率：
考虑到试样的应变均匀假设，有
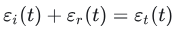
得到试样的应变率为：
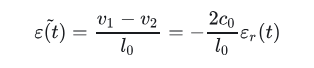
再对时间积分，得到试样的应变：
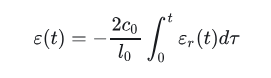
同时，试样的应力可以从试样与透射杆界面上的合力求出：
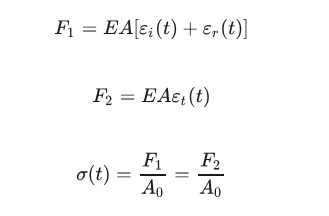
上述公式只用到反射透射或反射入射两组应变信号，就能得出试样的应变率、应变和应力，所以这套公式被称为SHPB的两波公式。
只要把任一时刻的应力和应变联系起来，就得到相应于某一应变率下的试样材料的应力-应变关系。
但是，实际测试发现，上述均匀变形的假设再快速加载情况下不是完全正确的。
当处在测量的最初阶段时，因为应力波在试件中反射次数不多，试样尚达不到均匀应力状态。
因此，可以采用两界面上的平均力计算试样中的应力：
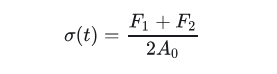
相应的，试样中的应力、应变率及应变可以用三组应变信号表示出来：
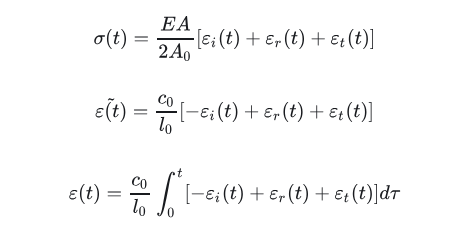
上述公式只用到三组应变信号得出试样的应变率、应变和应力，所以这套公式被称为SHPB分析的三波公式。
同样地，只要把任一时刻的应力和应变联系起来，就得到相应于某一应变率下的试样材料的应力-应变关系。